Segundo Previo de Medición Electrónica 2017-2 (UFPS)
Electronic Measurement Midterm 2017-2 (UFPS)
Un video explicativo del paso a paso que se verá a continuación:
Explicación:
Para trabajar con la herramienta Curve Fitting de Matlab, es necesario primero que nada cerciorarse de que el toolbox o la app se encuentra entre las instaladas, ya que es una herramienta adicional (add-on) de Matlab.
Ahora procederemos a crear nuestros vectores, que serán los valores en X y Y. Para este punto, los valores de la variable independiente corresponde a la distancia D, expresada en Centímetros y los valores de la variable dependiente corresponde al potencial V, expresado en Voltios.
Ahora procedemos a abrir la app de Curve Fitting:
Ya dentro del toolbox o app de Curve Fitting, procederemos a darle un nombre (Fit name), que en este caso le puse V vs D, para enfatizar el hecho de qué tipo de gráfica es. Luego procederemos a seleccionar los datos que deseemos para cada uno de los ejes, que en este caso sólo es X y Y (la variable D para X y la variable V para Y)
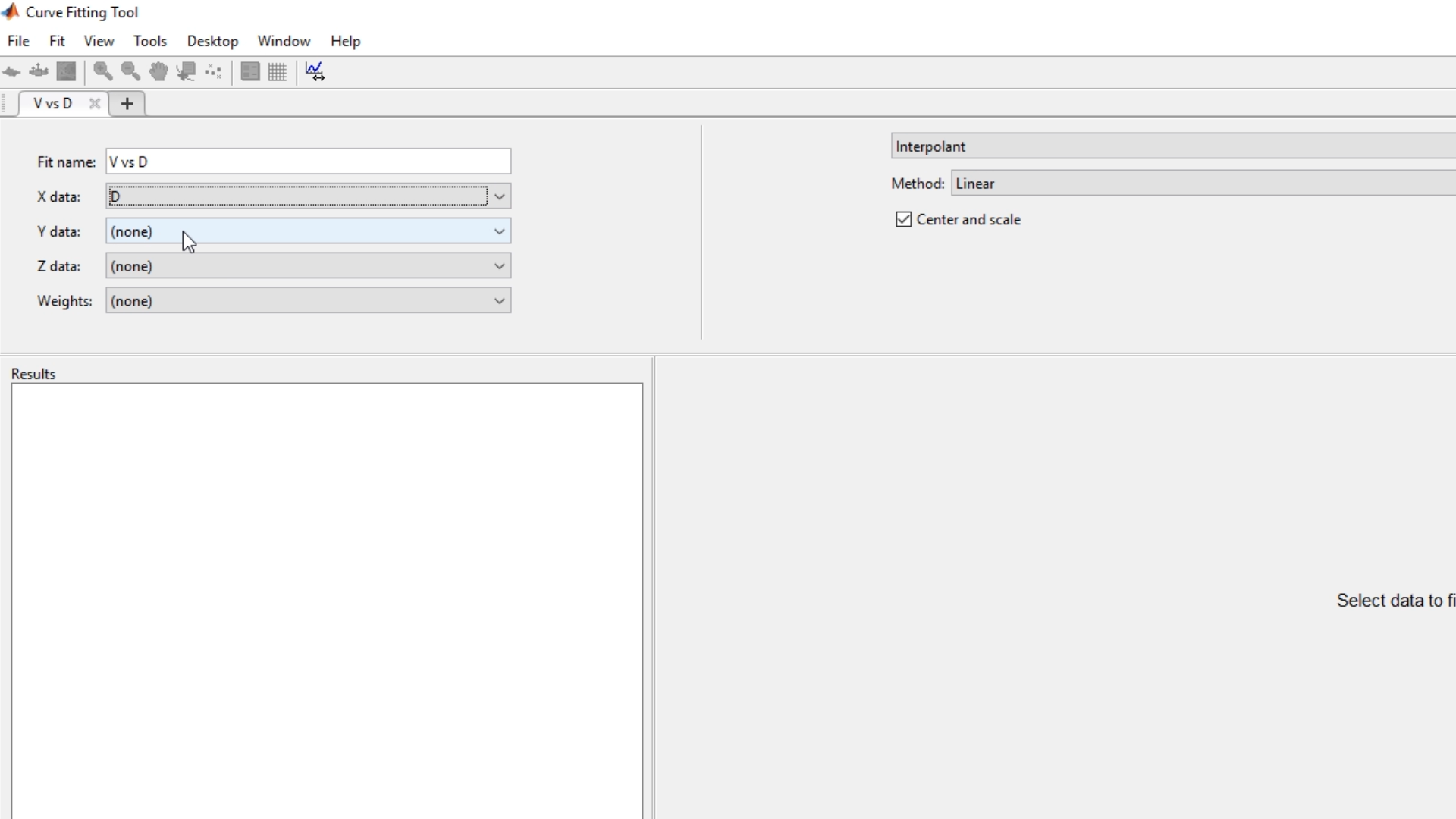
Por defecto, el toolbox nos mostrará la linealización de esa gráfica, como se puede ver a continuación:
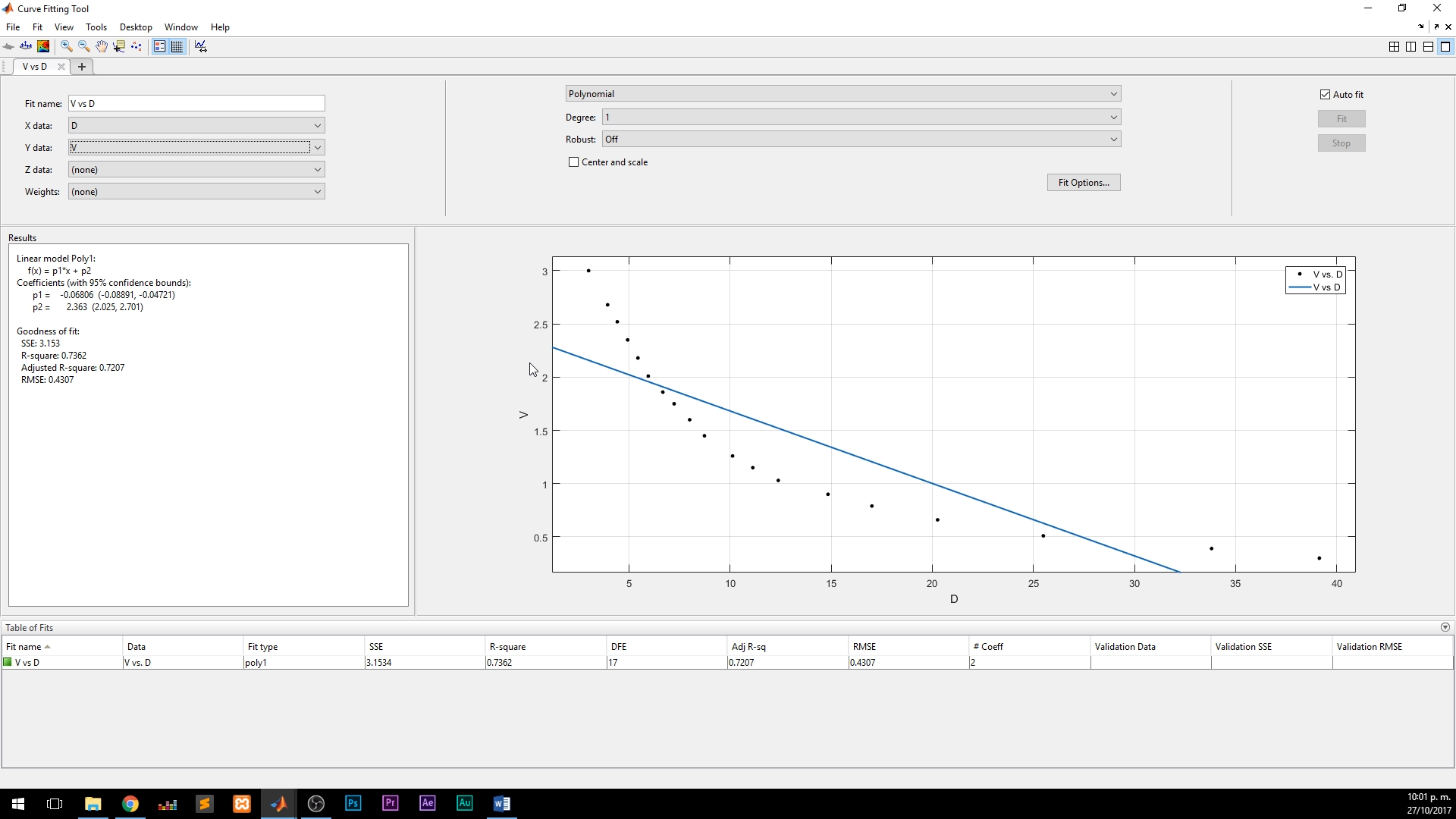
Al lado izquierdo, debajo de donde seleccionamos los datos, el toolbox nos dará los coeficientes del modelo lineal (de la forma y = mx+b, presentado en el toolbox como f(x) = p1*x + p2). En este caso, el valor de la pendiente es -0.06806 y el de la constante del intercepto es 2.363, tal y como se ve a continuación:
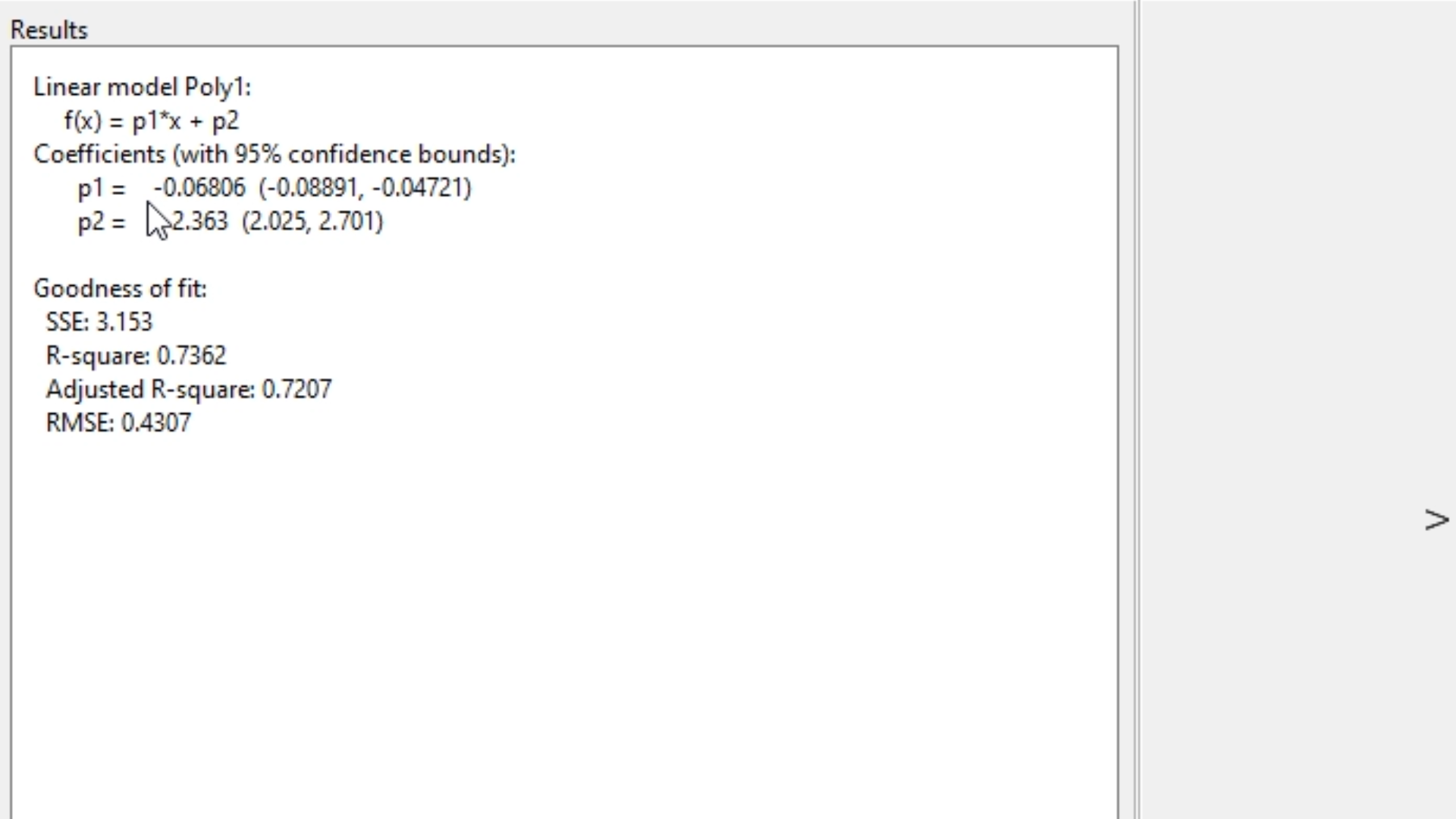
En el centro, podremos seleccionar el grado de la ecuación del polinomio (de 1 a 9 coeficientes):
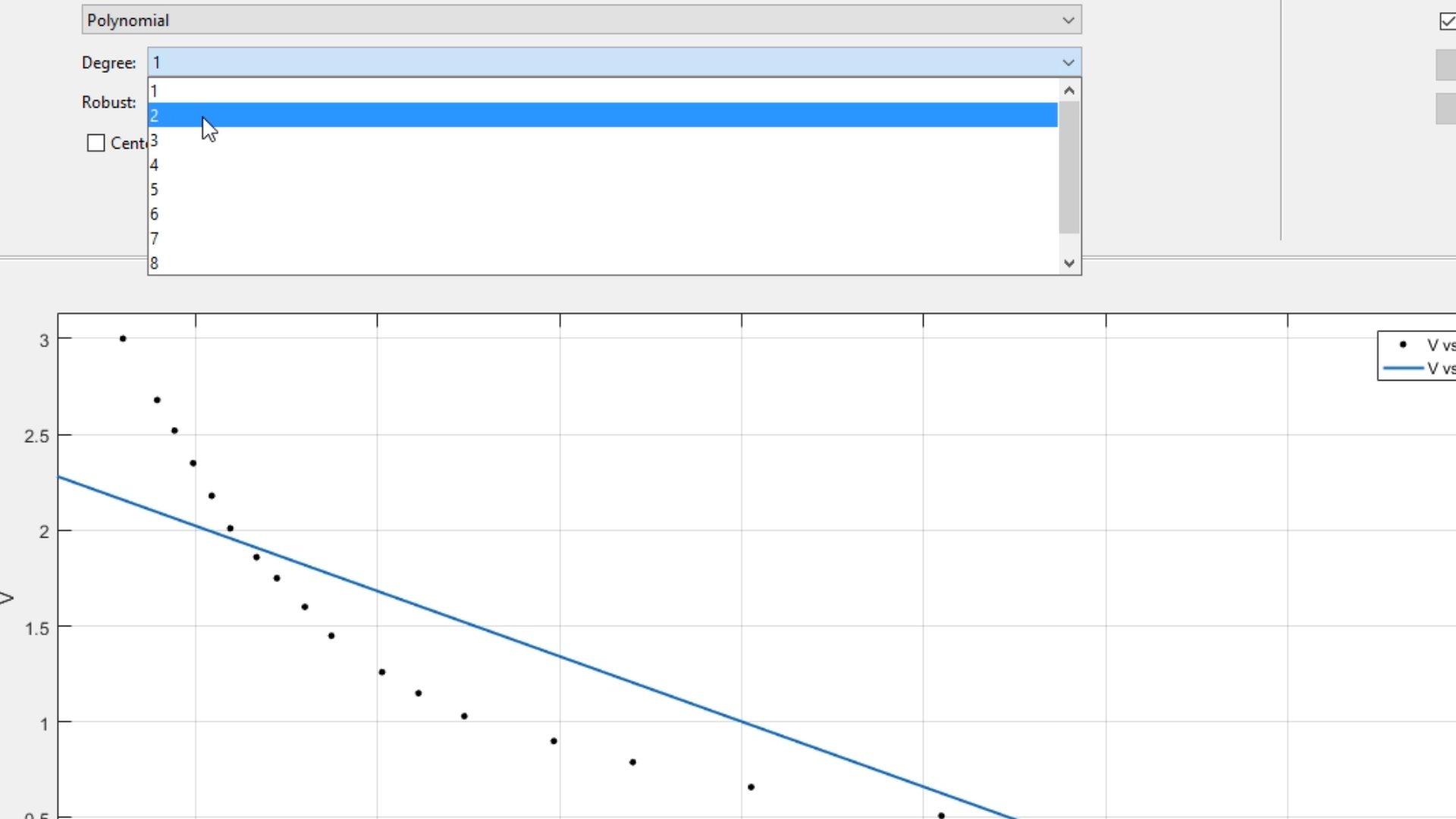
Por ejemplo, seleccionando 2, nos da como resultado la siguiente gráfica:
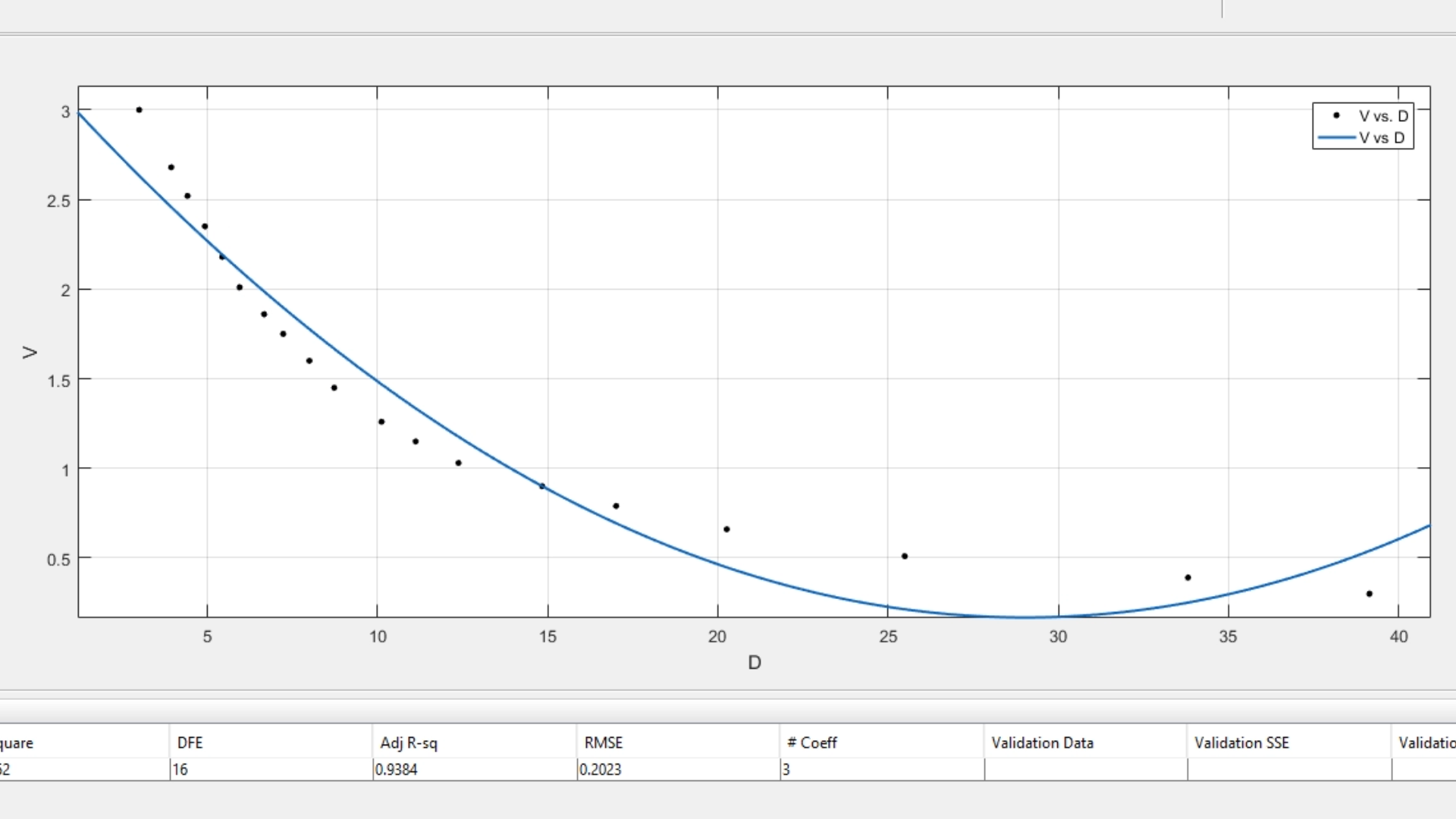
En el primer menú desplegable en el centro del toolbox de Curve Fitting podemos elegir el modelo que deseemos usar, por ejemplo, interpolar, que básicamente sigue consecutivamente los puntos creando líneas rectas (este método aunque hubiera podido ayudar a resolver el punto 5 del segundo previo, no permite escoger datos "por trozos", es decir, crear 4 rectas)
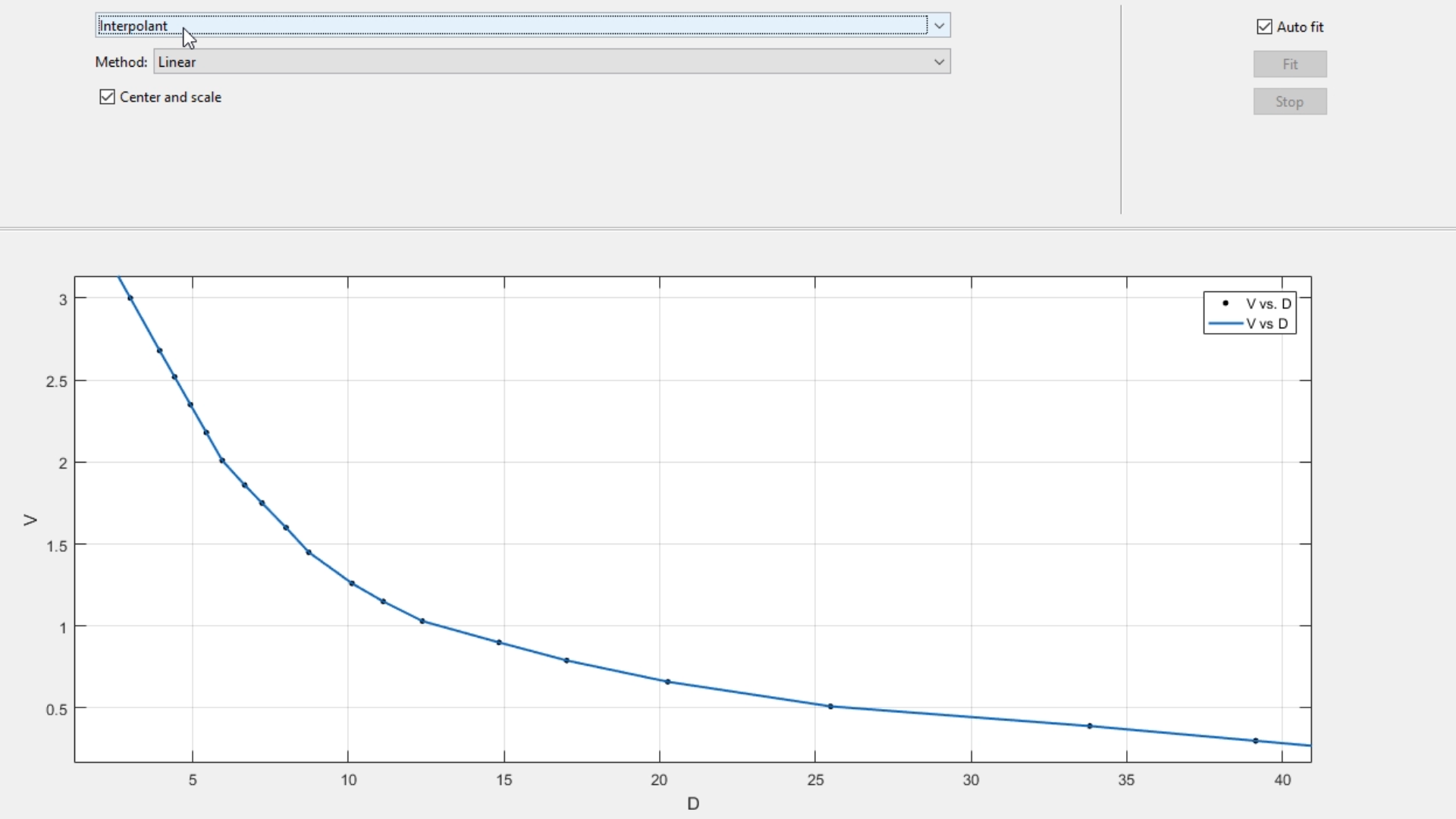
Tenemos la posibilidad de explorar otros modelos que puedan ayudarnos a descubrir el comportamiento de la recta, como el modelo exponencial:
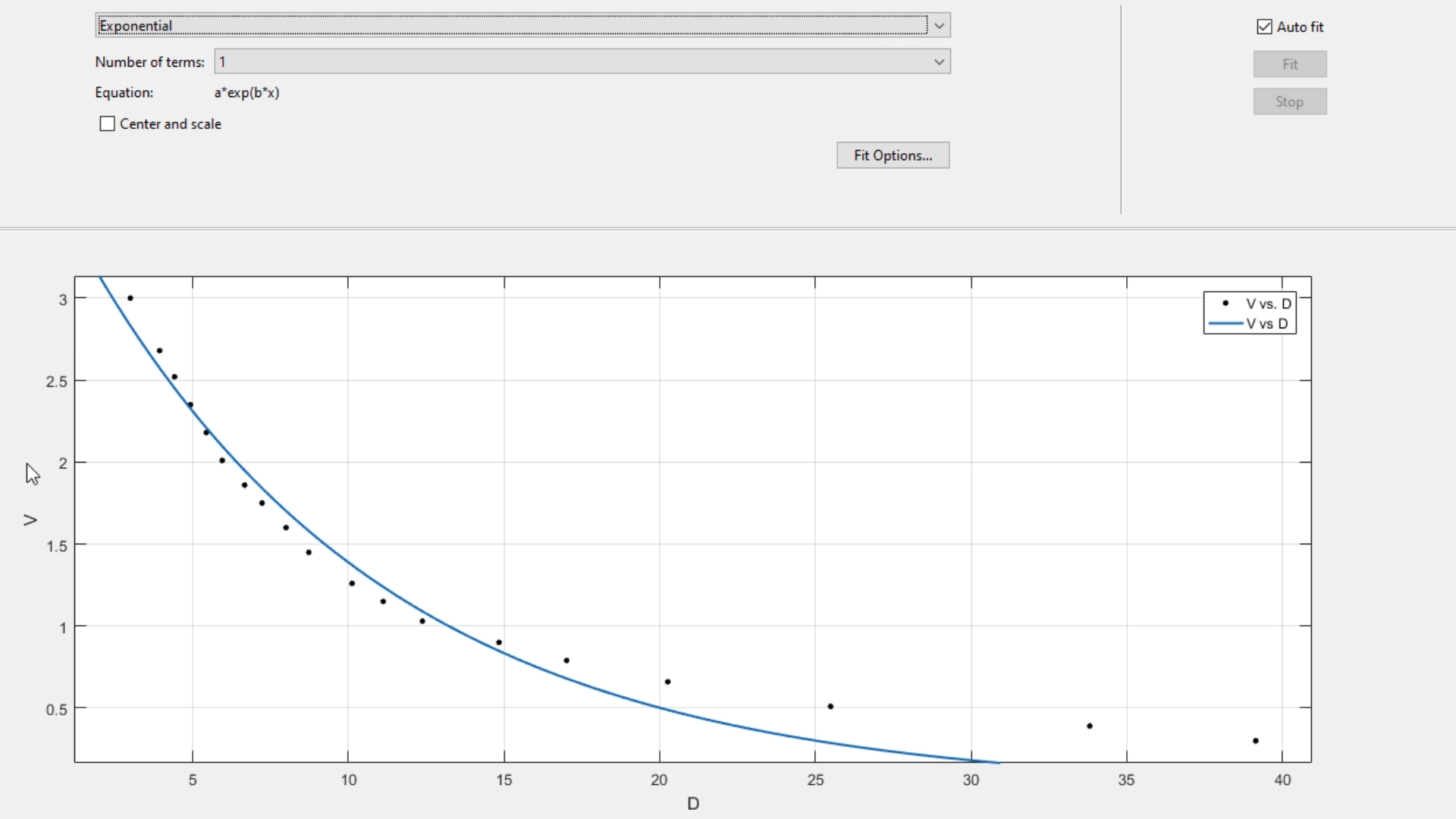
O el modelo de Fourier (que se aleja bastante de una gran cantidad de puntos, que cuyo comportamiento no está ni cerca de ser el de la gráfica original):
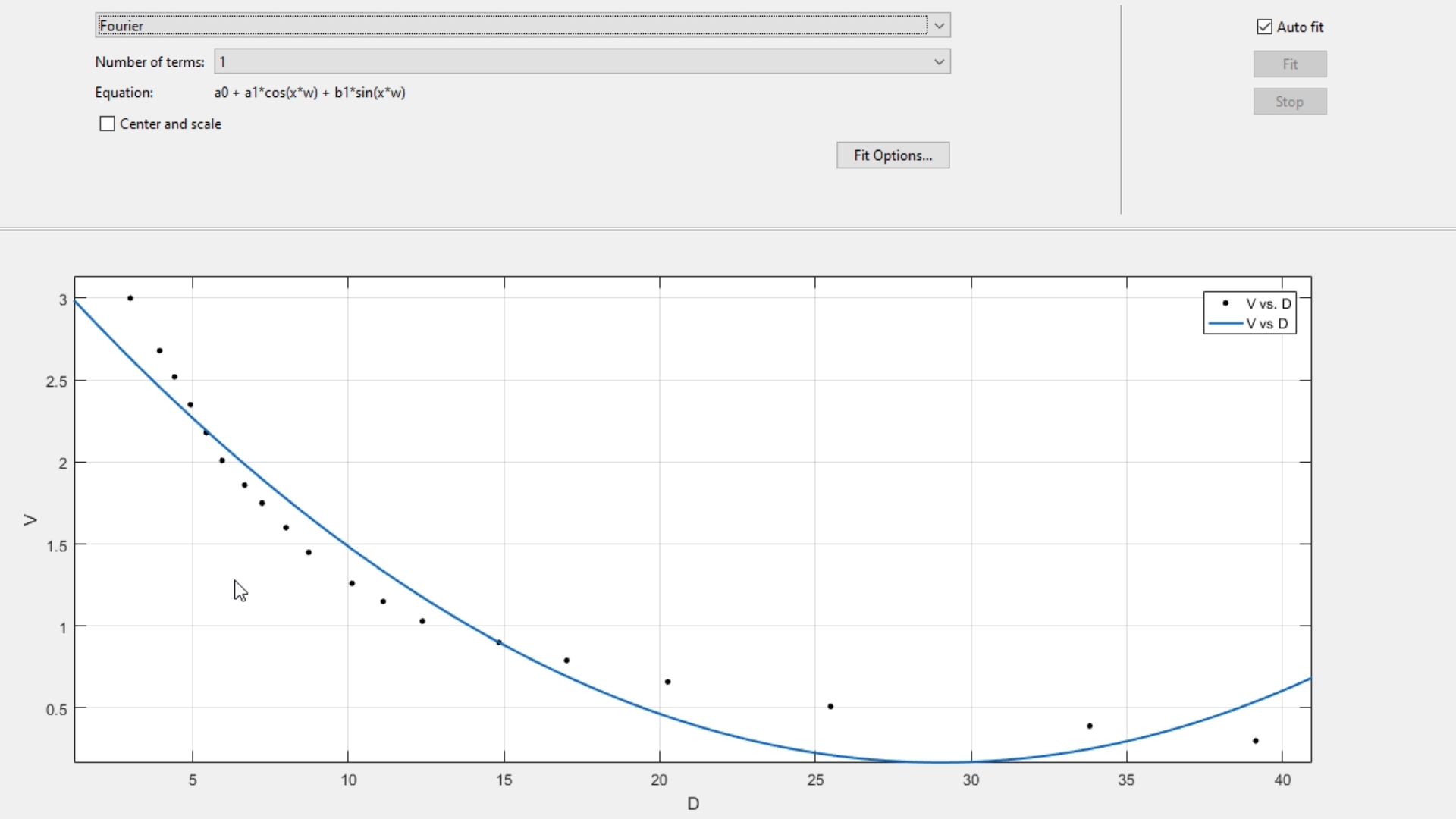
Finalmente, un modelo que parece describir con bastante cercanía el conjunto de datos, es el modelo Racional (Radical)
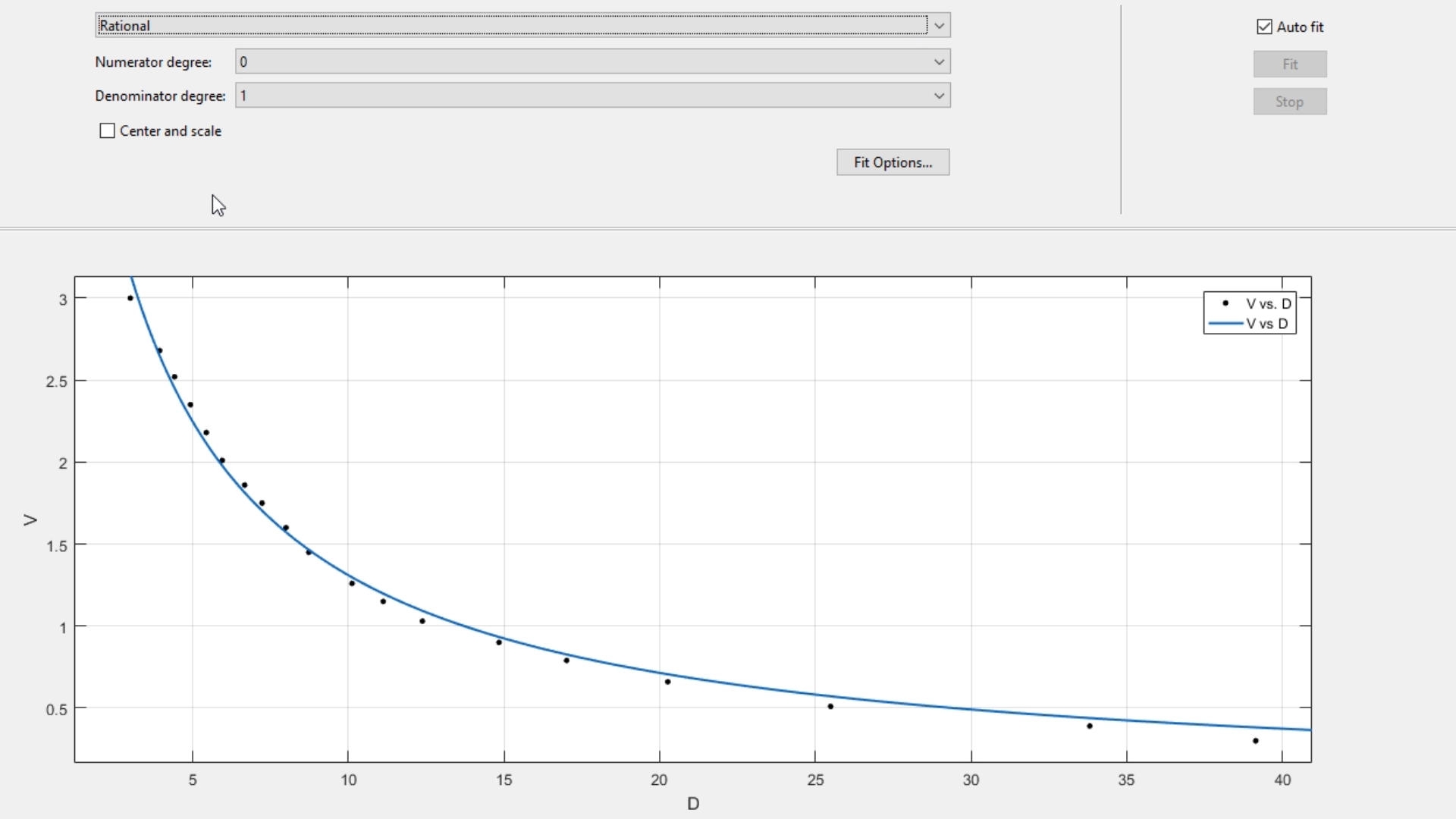
Podremos ver qué tanto se acerca este modelo a nuestro conjunto de datos usando la gráfica de los residuos, visible a través del menú View -> Residuals Plot:
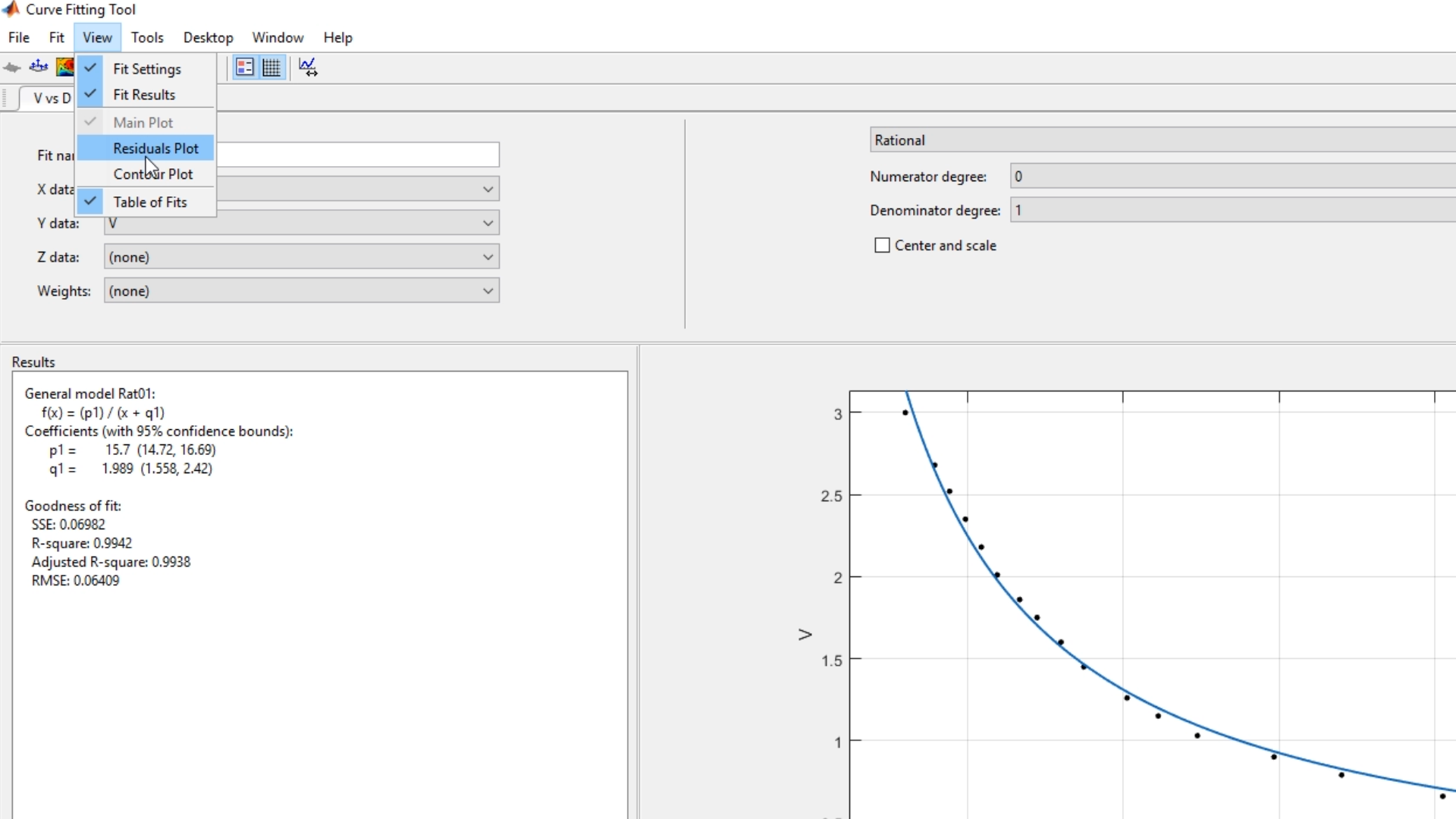
Así podremos ver junto a la gráfica principal, la gráfica de sus valores residuos, que tal y como se aprecia, son décimas y hasta centésimas lo que separa este modelo del conjunto de datos:
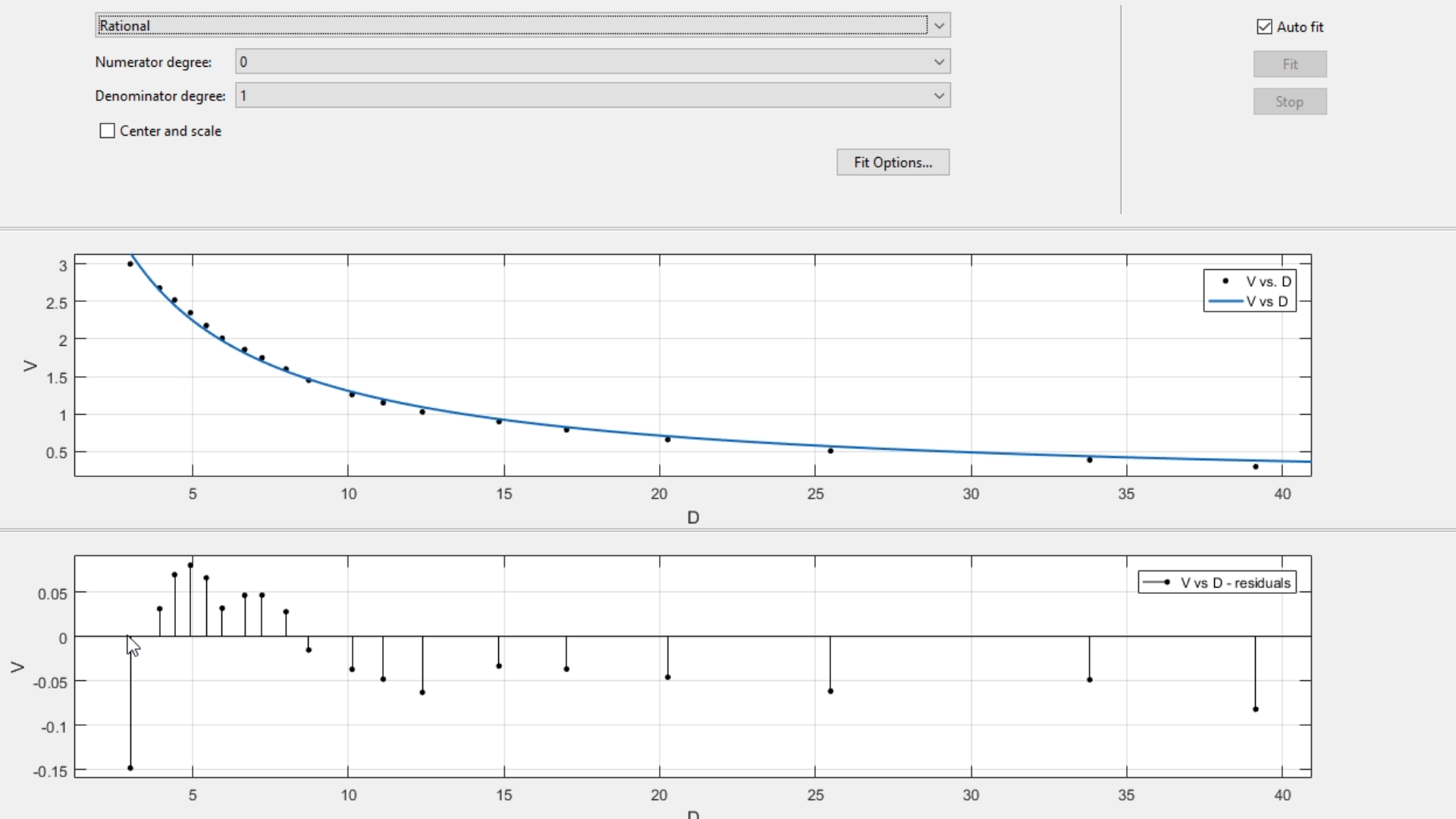
Ya con nuestra figura en el toolbox de Curve Fitting, podremos exportar esta gráfica a la función de figura, propia de Matlab, con la que podremos realizar más cosas, para hacerlo, nos dirigimos a File -> Print to Figure:
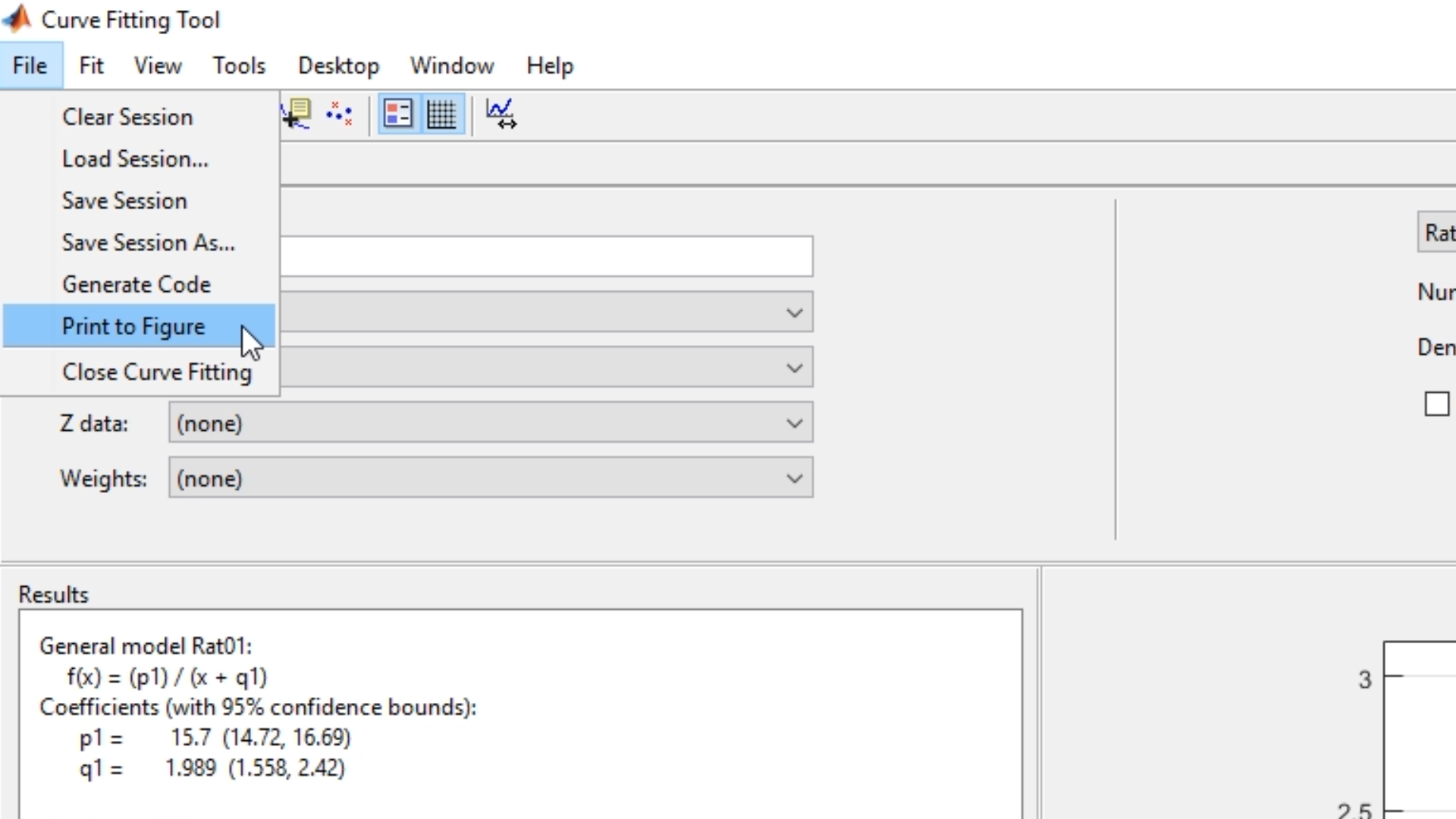
Ya dentro de Figure, en Matlab, podremos acceder a todas las funciones, como la de extrapolación, ubicada en la barra de herramientas, debajo del menú de la figura:
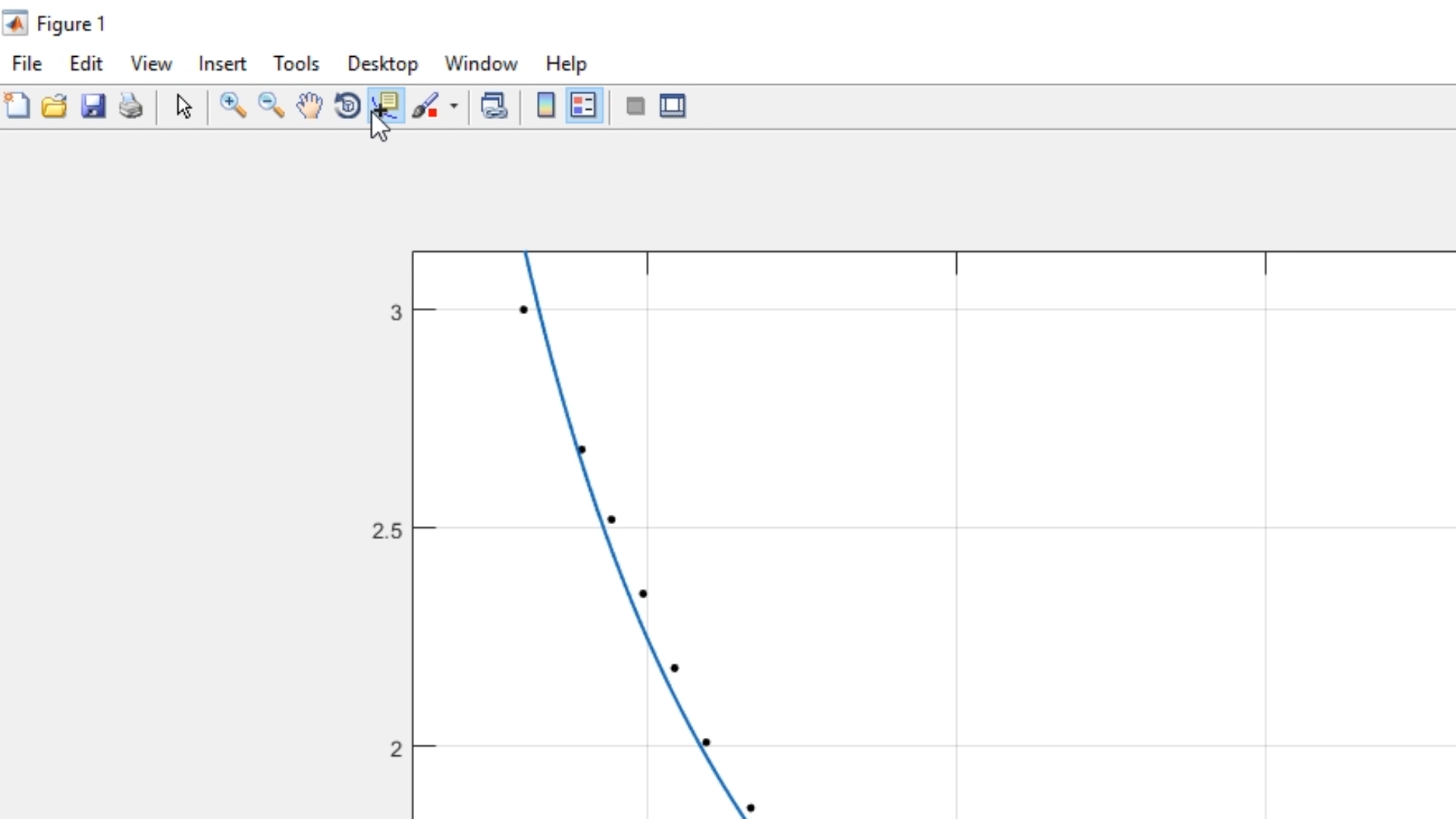
Ya con la herramienta, podremos seleccionar cualquier parte de la gráfica y obtener sus valores de X y Y (o D y V en nuestro caso):
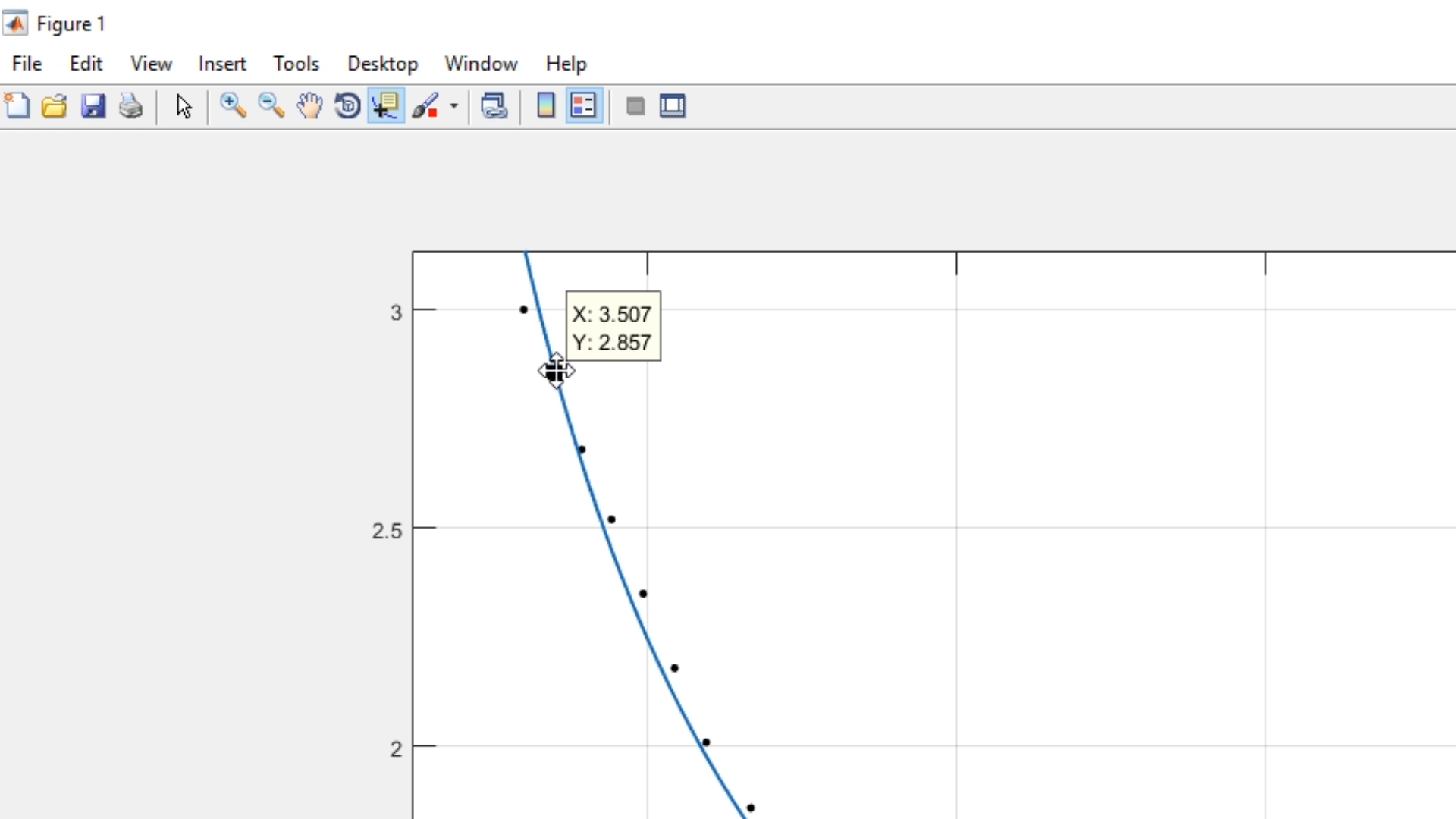
Y finalmente, una de las cosas más útiles de exportar a Figure de Matlab, es el de poder copiar la figura sin necesidad de usar herramientas externas o realizar un proceso un poco más largo (como imprimir pantalla y recortar la figur):
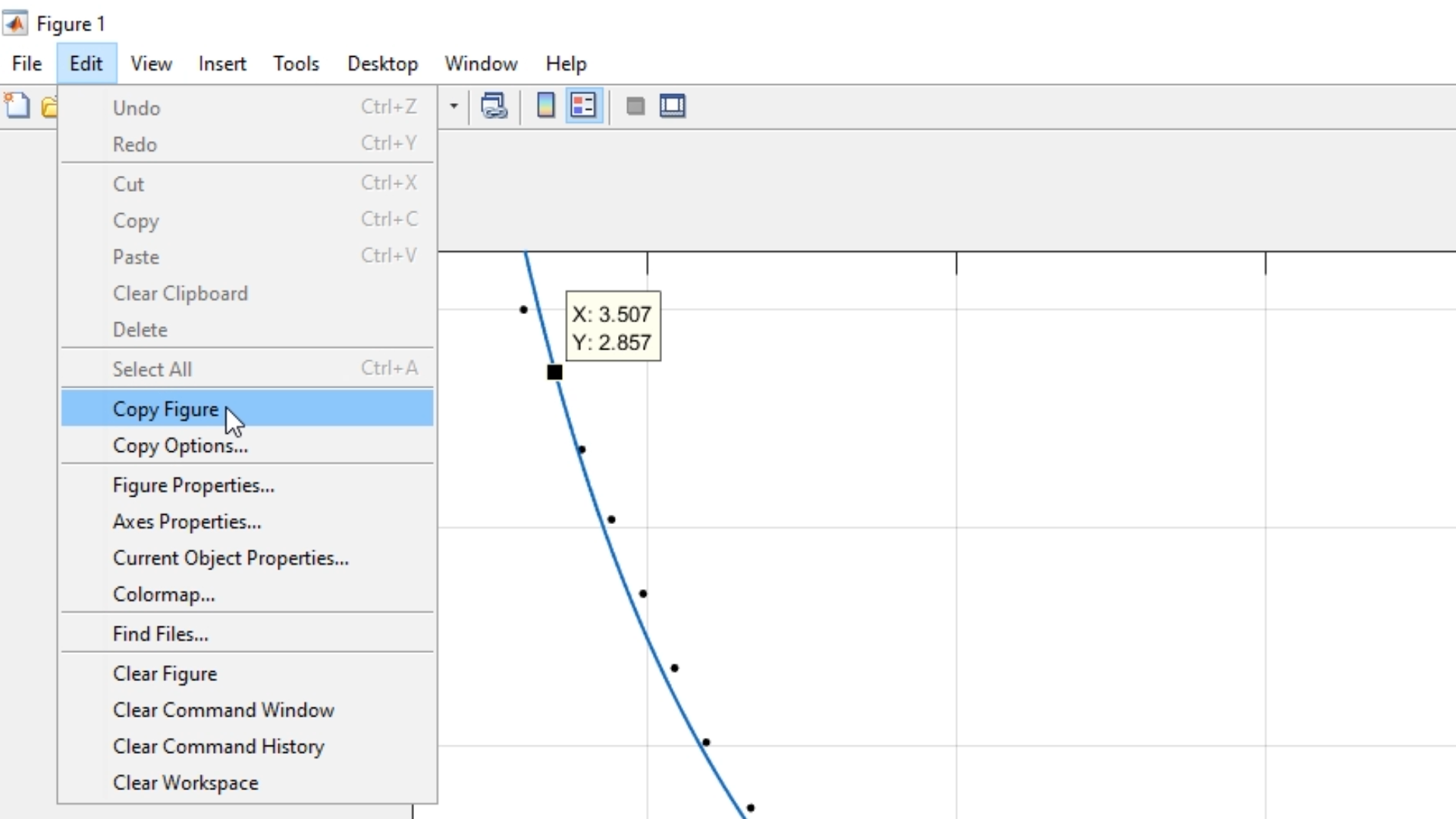
La herramienta de Curve Fitting finalmente nos muestra ser una herramienta muy poderosa para trabajar con un conjunto de datos e ir encontrando el modelo matemático o la tendencia que cumple ese conjunto de datos, muy útil en las etapas de planificación de un experimento.
Espero que esta explicación haya sido de ayuda.
- Linealice las siguientes funciones:
- \(R=\ a\ e^\frac{b}{T}\)
- Llamamos \(T’\) a \(\frac{1}{T}\), \(R’\) a \(Ln(R)\) y a \(Ln(a)\) lo llamamos \(a’\), así: $$R\prime\ =\ bT\prime\ +\ a\prime$$
- Realizamos el inverso de la ecuación para que la ecuación quede de la forma correcta: $$\frac{1}{Ln(R)}\ =\ \frac{T}{b}\ +\ \frac{1}{Ln(a)}$$
- \( M\ =\ \sqrt{ct \ +\ d} \)
- \( P\ =\ e\ +\ \frac{g}{T} \)
- \( PV^n\ =\ k \)
- Para la función del literal c) dibujar la gráfica, si \(e\ =\ 3,8x{10}^5\) y \({g\ =\ -1,02x10}^8\) entre el rango de valores T=273K y T=450K.
- Especificar cada una de las etapas, que se deben formular en la solución de los siguientes problemas:
- Determinar el modelo circuital paralelo de un capacitor de aceite
- Definición y defensa del problema o investigación
- Análisis preliminar del problema
- Planificación del experimento
- Evaluación del experimento
- Conclusiones
- Un condensador ideal de capacidad C, por el cual no pasa corriente, es decir, tiene conductancia nula (o resistencia infinita)
- Una resistencia ideal R, que no almacena carga alguna, es decir, sin capacidad
- Determinar los valores R y C de un circuito serie mediante un generador de frecuencia variable
- Definición y defensa del problema
- Análisis preliminar del problema
- Planificación del experimento
- Evaluación del experimento
- Conclusiones
- Utilizando la técnica de mínimos cuadrados linealice los siguientes conjuntos de datos:
- Para las siguientes tablas, agregaremos inmediatamente las columnas que nos serán útiles para realizar el análisis de los mínimos cuadrados.
- Utilice el ajuste de mínimos cuadrados para linealizar la siguiente curva utilizando 4 líneas rectas
- Investigue el uso del toolbox o apps de Matlab “curve fitting” y realice el ajuste de curva más adecuado para la curva del punto 5. Realice un tutorial paso a paso donde muestre los resultados.
Para linealizar esta función se aplica logaritmo natural a cada lado:
$$Ln(R)\ =\ \frac{b}{T}\ +\ Ln(a)$$En este momento tenemos dos opciones:
Podremos llamar a \(\frac{1}{Ln(R)} R’\) y a \(\frac{1}{Ln(a)}\) llamarlo \(a’\), para tener ecuación así:
$$R\prime\ =\ \frac{1}{b}T\ +\ a\prime$$Para linealizar esta ecuación sólo tendremos que elevar ambos lados al cuadrado, y llamar \(M\prime\) a \(M^2\):
$$M^2\ =\ ct\ +\ d\ \Rightarrow\ M\prime\ =\ ct\ +\ d$$Para linealizar esta función llamamos \(T’\) a \(\frac{1}{T}\):
$$P\ =\ gT\prime\ +\ e$$Para linealizar esta función, debemos tratar de llevarla al modelo potencial:
$$P\ =\ \frac{k}{V^n}$$Ahora, como necesitamos a \(V^n\) en el numerador para poderla linealizar, llamaremos \(P\prime\) a \(\frac{1}{P}\):
$$P\prime\ =\ \frac{1}{k}\ V^n$$Ahora la linealizaremos a través de los logaritmos:
$$log(P\prime)\ =\ n\ log(V)\ +\ log(\frac{1}{k})$$Y nuevamente haremos cambio de variable, de la siguiente forma:
$$P^{\prime\prime}=log{\left(P^\prime\right)}$$ $$V^\prime=log{\left(V\right)}$$ $$k\prime\ =log(\frac{1}{k})$$Entonces la ecuación quedaría de la siguiente forma:
$$P\prime\prime\ =\ nV\prime\ +\ k\prime$$La siguiente gráfica es la representación de la función sin su linealización utilizando Matlab.
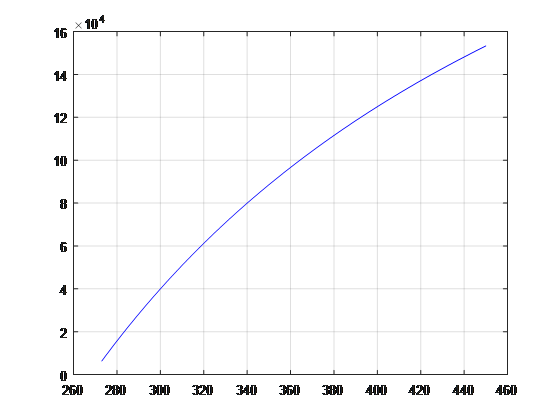
Utilizando “Data Cursor”, una de las herramientas en el visualizador de gráficas de Matlab, se seleccionaron los siguientes valores de T con sus respectivos valores de P:
T |
273 |
303 |
333 |
363 |
393 |
423 |
453 |
P |
6374 |
\( 4.337x{10}^4 \) |
\( 7.369x{10}^4 \) |
\( 9.901x{10}^4 \) |
\( 1.205x{10}^5 \) |
\( 1.389x{10}^5 \) |
\( 1.548x{10}^5 \) |
Los datos fueron llevados a las funciones polyfit y polyval de Matlab para realizar la gráfica:
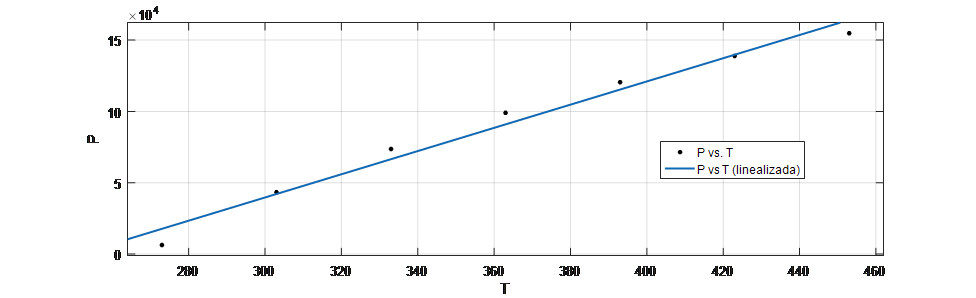
La ecuación de la recta está dada por: \(P(T)=813.3T-\ 2.043x{10}^5\) (A partir de \(f(x)\ =\ p1\ast x\ -\ p2\))
Grupo B Asignado al grupo en el que estoy
Un capacitor de aceite es un dispositivo capaz de almacenar energía sustentando un campo eléctrico, cuyo dieléctrico en este caso es el aceite, esto debido a que el aceite es de utilidad para ser usado con altos voltajes en corriente alterna (AC) o doble voltajes (AC/DC), con altos picos de voltaje, altos picos de corriente y cuando el tiempo de operación sea de larga duración. Por otra parte, el uso de estos capacitores o condensadores se ha visto reducido por la cantidad de contaminación que llegan a producir.
El modelo con el que se identifica el capacitor (de una forma general, independiente de su dieléctrico, es aquel en el que se tienen dos placas perfectamente conductoras de sección S, separadas una distancia a entre las cuales hay un dieléctrico de permitividad \(\varepsilon\) y con una pequeña conductividad \(\sigma\). Entre las placas se establece una d.d.p. constante por medio de una fuente de f.e.m \(\epsilon\), tal y como se ilustra en la figura a continuación:
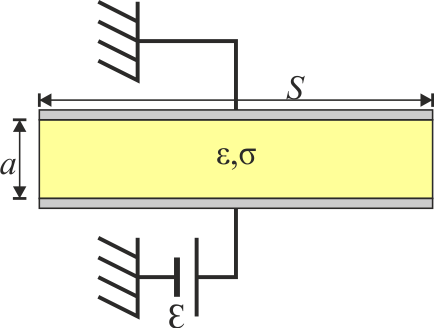
Para analizar el capacitor estudiaremos la corriente que fluye a través de él, así como sus densidades de corriente, para hallar la capacitancia y posteriormente su modelo circuital. En el medio material existe una densidad de corriente proporcional al campo, según la ley de Ohm:
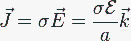
Esto quiere decir que el medio dieléctrico, al no ser perfectamente aislante, es atravesado por una intensidad de corriente
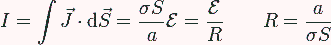
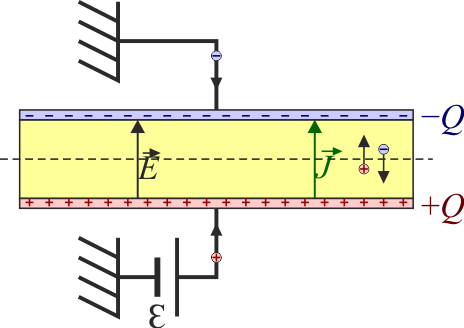
El que haya una corriente no quiere decir que las placas estén descargadas. Como en cualquier condensador plano habrá una carga:
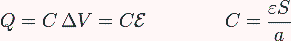
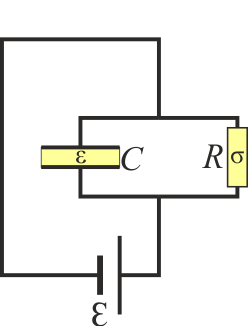
Ahora llevaremos el circuito a su versión equivalente. Este elemento es tanto un capacitor C (caracterizado por una carga y una energía almacenada) como una resistencia R (caracterizada por una corriente y una potencia disipada por efecto Joule). La diferencia de potencial entre los extremos de la resistencia es la misma que entre los del condensador, por lo que ambos elementos están en paralelo.
Si se conecta una fuente real, el circuito equivalente se complica:
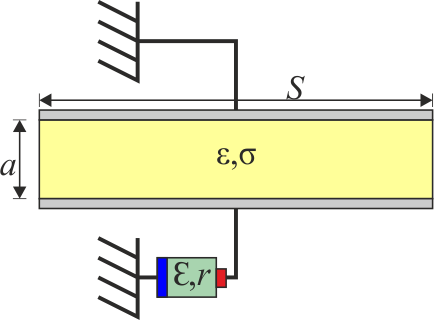
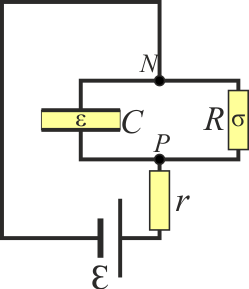
Aunque el sistema real está formado por dos elementos (la fuente real y el condensador con pérdidas), el circuito equivalente está formado por cuatro: la fuente ideal y la resistencia interna, puestos en serie y el condensador ideal y la resistencia ideal, puestos en paralelo.
La diferencia de potencial entre las placas ya no coincide con la fuerza electromotriz, sino que:
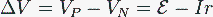
Se sigue cumpliendo que la diferencia de potencial entre las placas es proporcional a la corriente que circula por el material
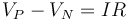
Igualando y despejando obtenemos la corriente
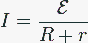
y la d.d.p.
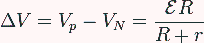
Una vez que tenemos la diferencia de potencial, tenemos la carga en las placas, que ahora es dependiente de la resistencia del elemento:
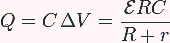
Igualmente hallamos el campo entre las placas
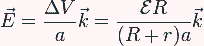
La densidad de corriente
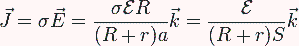
La energía almacenada
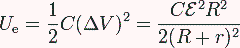
Y la potencia disipada
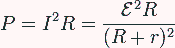
Sin la conexión de la fuente, el circuito equivalente a un condensador real con pérdidas es una asociación en paralelo de dos elementos:
De esta forma, en el circuito se separan los efectos de almacenamiento de carga y de flujo de carga. De la misma manera, se separan el almacenamiento de energía y la disipación de energía por efecto Joule.
De todas maneras, hay que insistir, no obstante, que aunque el circuito equivalente tenga dos elementos, en realidad se trata de un solo dispositivo físico. Una cosa es el sistema real y otra su modelo circuital.
De igual forma, que el capacitor sea de aceite, electrolítico o cerámico, sólo afecta su capacidad de carga más no su modelo circuital.
Información gracias a:
Para analizar los valores de R y C, debemos considerar un circuito RLC completo, y además analizar el circuito teniendo en cuenta la frecuencia, por lo tanto, los valores se definirán a partir de la ecuación que dice que la frecuencia angular es igual a dos veces pi por la frecuencia \( \omega\ =\ 2\pi f\ \))
Una señal alterna (proveniente de una fuente de tensión de corriente alterna) puede ser considerada como un generador de frecuencia variable, y al conectar un circuito RLC en serie a esta, hay en un efecto de ésta en cada uno de los componentes. En el condensador aparecerá una reactancia capacitiva y en la bobina una reactancia inductiva, dadas por las ecuaciones:
$$XL\ =\ 2\ \ast\ \pi\ast\ f\ \ast\ L\ \ $$ $$XC\ =\ \frac{1}{2\ \ast\ \pi\ \ast\ f\ \ast\ C}$$Como se puede ver los valores de estas reactancias depende de la frecuencia de la fuente. A mayor frecuencia, XL es mayor, pero XC es menor y viceversa.
Hay una frecuencia para la cual el valor de la XC y XL son iguales. Esta frecuencia se llama frecuencia de resonancia y se obtiene de la siguiente fórmula:
$$FR\ =\ \frac{1}{2\pi\ \sqrt{(L\ast C)}}$$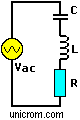
En resonancia como los valores de XC y XL son iguales, se cancelan y en un circuito RLC en serie la impedancia que ve la fuente es el valor de la resistencia. A frecuencias menores a la de resonancia, el valor de la reactancia capacitiva es grande y la impedancia es capacitiva. A frecuencias superiores a la de resonancia, el valor de la reactancia inductiva crece y la impedancia es inductiva.
La importancia de este tipo de circuitos es que son utilizados para seleccionar bandas de frecuencias y para rechazar otras. Cuando se está en la frecuencia de resonancia la corriente por el circuito es máxima.
Información gracías a: Electrónica Unicrom
Xi |
Yi |
1 |
1.5 |
2 |
2.0 |
3 |
4.0 |
5 |
4.6 |
6 |
4.7 |
8 |
8.5 |
9 |
8.8 |
10 |
9.9 |
Para aplicar la técnica de los mínimos cuadrados realizaremos la siguiente tabla:
Xi |
Yi |
\({Xi}^2\) |
Xi * Yi |
1 |
1.5 |
1 |
1.5 |
2 |
2.0 |
4 |
4.0 |
3 |
4.0 |
9 |
12.0 |
5 |
4.6 |
25 |
23.0 |
6 |
4.7 |
36 |
28.2 |
8 |
8.5 |
64 |
68.0 |
9 |
8.8 |
81 |
79.2 |
10 |
9.9 |
100 |
99 |
\( \sum X i\ =\ 44 \) |
\( \sum Y i\ =\ 44 \) |
\( \sum{Xi}^2\ =\ 320 \) |
\( \sum{Xi\ \ast\ Yi}\ =\ 314.9 \) |
Entonces, sabiendo que N es la cantidad de datos (N = 8), podemos decir que la incertidumbre \(\Delta\) es:
$$\Delta = 8 * (320) - {(\mathbf{44})}^\mathbf{2} = 624$$ $$m\ =\ \frac{N\sum_{i=1}^{N}{X_iY_i-\sum_{i=1}^{N}{X_i\sum_{i=1}^{N}Y_i}}}{\Delta}\ =\ \frac{(8\ \ast\ 314.9)\ -\ (44\ \ast\ 44)}{624}$$ $$m\ =\ 0.935$$ $$b=\frac{\sum_{i=1}^{N}{{X_i}^2{\sum_{i=1}^{N}Y}_i-\sum_{i=1}^{N}{X_i\sum_{i=1}^{N}{X_iY}_i}}}{\Delta}\ =\ \frac{(320\ \ast\ 44)\ -\ (44\ \ast\ 314.9)}{624}$$ $$b=\ 0.359$$ $$\sigma_y=\sqrt{\frac{1}{N-2}\sum_{i=1}^{N}{(Y_i-b-m{X_i)}^2}}$$ $$\sum_{i=\mathbf{1}}^{N}{(Y_i-b-m{X_i)}^\mathbf{2}}\ \ $$ $$={(1,5-0.359-0.935\ast1)}^2+{(2-0.359-0.935\ast2)}^2+{(4-0.359-0.935\ast3)}^2+{(4.6-0.359-0.935\ast5)}^2+{(4.7-0.359-0.935\ast6)}^2+{(8.5-0.359-0.935\ast8)}^2+{(8.8-0.359-0.935\ast9)}^2+{(9.9-0.359-0.935\ast10)}^2$$ $$=0.0424 + 0.0524 + 0.699 + 0.188 + 1.61 + 0.437 + 6.76\ast{10}^{-4} + 0.0365$$ $$=3.066$$ $$\sigma_y=\sqrt{\frac{\mathbf{3}.\mathbf{066}}{\mathbf{8}-\mathbf{2}}}=\mathbf{0}.\mathbf{715} $$Ahora hallaremos las incertidumbres para la pendiente (m) y para la constante del intercepto (b):
$$\mu_m=\sigma_y\sqrt{\frac{N}{\Delta}}=0.715\sqrt{\frac{8}{624}}=0.081$$ $$\mu_b=\sigma_y\sqrt{\frac{\sum_{i=1}^{N}{X_i}^2}{\Delta}}=0.715\sqrt{\frac{320}{624}}=0.512$$La ecuación de la recta resultante sería:
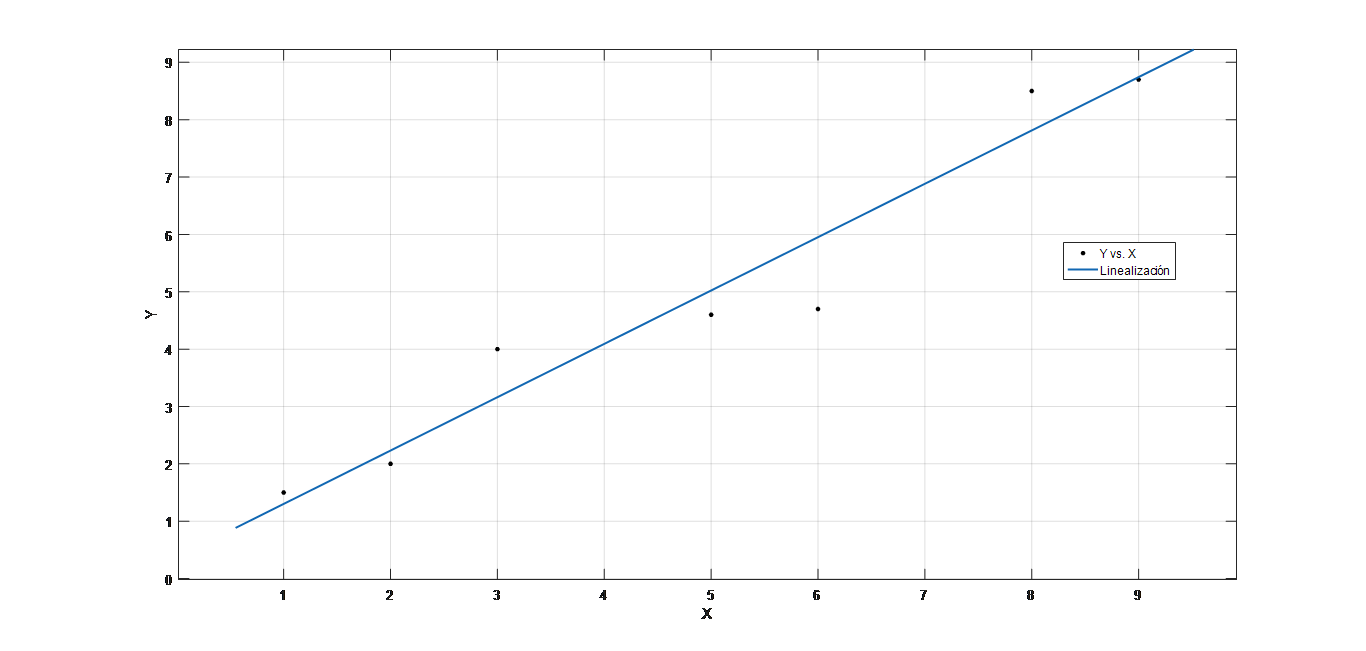
$$\mathbf{Y}=\left(\mathbf{0}.\mathbf{935}\pm\mathbf{0}.\mathbf{081}\right)\mathbf{X}+(\mathbf{0}.\mathbf{359}\pm\mathbf{0}.\mathbf{512})$$A continuación, se visualiza la gráfica con su linealización:
Temperatura (°C) |
Voltaje (mV) |
\({Ti}^2\) |
Ti * Vi |
47 |
749 |
2209 |
35203 |
45,2 |
774 |
2043,04 |
34984,8 |
44,1 |
799 |
1944,81 |
35235,9 |
43,1 |
823 |
1857,61 |
35471,3 |
42,2 |
852 |
1780,84 |
35954,4 |
41,2 |
877 |
1697,44 |
36132,4 |
40,4 |
906 |
1632,16 |
36602,4 |
39,3 |
935 |
1544,49 |
36745,5 |
38,4 |
970 |
1474,56 |
37248 |
37,4 |
999 |
1398,76 |
37362,6 |
36,4 |
1033 |
1324,96 |
37601,2 |
35,3 |
1068 |
1246,09 |
37700,4 |
34,5 |
1101 |
1190,25 |
37984,5 |
33,5 |
1136 |
1122,25 |
38056 |
32,5 |
1174 |
1056,25 |
38155 |
31,6 |
1209 |
998,56 |
38204,4 |
30,6 |
1248 |
936,36 |
38188,8 |
29,7 |
1287 |
882,09 |
38223,9 |
28,5 |
1331 |
812,25 |
37933,5 |
27,6 |
1370 |
761,76 |
37812 |
26,9 |
1413 |
723,61 |
38009,7 |
25,6 |
1458 |
655,36 |
37324,8 |
24,9 |
1502 |
620,01 |
37399,8 |
23,7 |
1547 |
561,69 |
36663,9 |
22,7 |
1595 |
515,29 |
36206,5 |
21,8 |
1642 |
475,24 |
35795,6 |
20,8 |
1692 |
432,64 |
35193,6 |
20 |
1740 |
400 |
34800 |
18,9 |
1793 |
357,21 |
33887,7 |
18 |
1847 |
324 |
33246 |
17,1 |
1901 |
292,41 |
32507,1 |
16,1 |
1956 |
259,21 |
31491,6 |
15,1 |
2008 |
228,01 |
30320,8 |
14,3 |
2066 |
204,49 |
29543,8 |
13,4 |
2120 |
179,56 |
28408 |
12,3 |
2174 |
151,29 |
26740,2 |
11,3 |
2239 |
127,69 |
25300,7 |
10,5 |
2297 |
110,25 |
24118,5 |
9,2 |
2354 |
84,64 |
21656,8 |
8,6 |
2385 |
73,96 |
20511 |
6,8 |
2507 |
46,24 |
17047,6 |
5,8 |
2566 |
33,64 |
14882,8 |
5 |
2629 |
25 |
13145 |
\( \sumT_i=\ 1107,3 \) |
\( \sum{V_i=}\ 66072 \) |
\( \sum{T_i}^2=34794,97 \) |
\( \sum{T_i\ast V_i}=\ 1415001,5 \) |
Las incertidumbres de la pendiente y el intercepto están dadas por:
$$\sigma_V=\sqrt{\frac{0.221}{43-2}}=0.0734$$ $$\mu_m=\sigma_V\sqrt{\frac{N}{\Delta}}=0.0734\sqrt{\frac{43}{270070.42}}=9.26*{10}^{-4}$$ $$\mu_b=\sigma_V\sqrt{\frac{\sum_{i=1}^{N}{T_i}^2}{\Delta}}=0.0734\sqrt{\frac{34794,97}{270070.42}}=0.0263$$Y la ecuación de la recta quedaría tal que:
$$V = (-0.0456 \pm 9.26*{10}^{-4} )T + (2.71 \pm 0.0263)$$A continuación, se detalla la gráfica con su linealización:
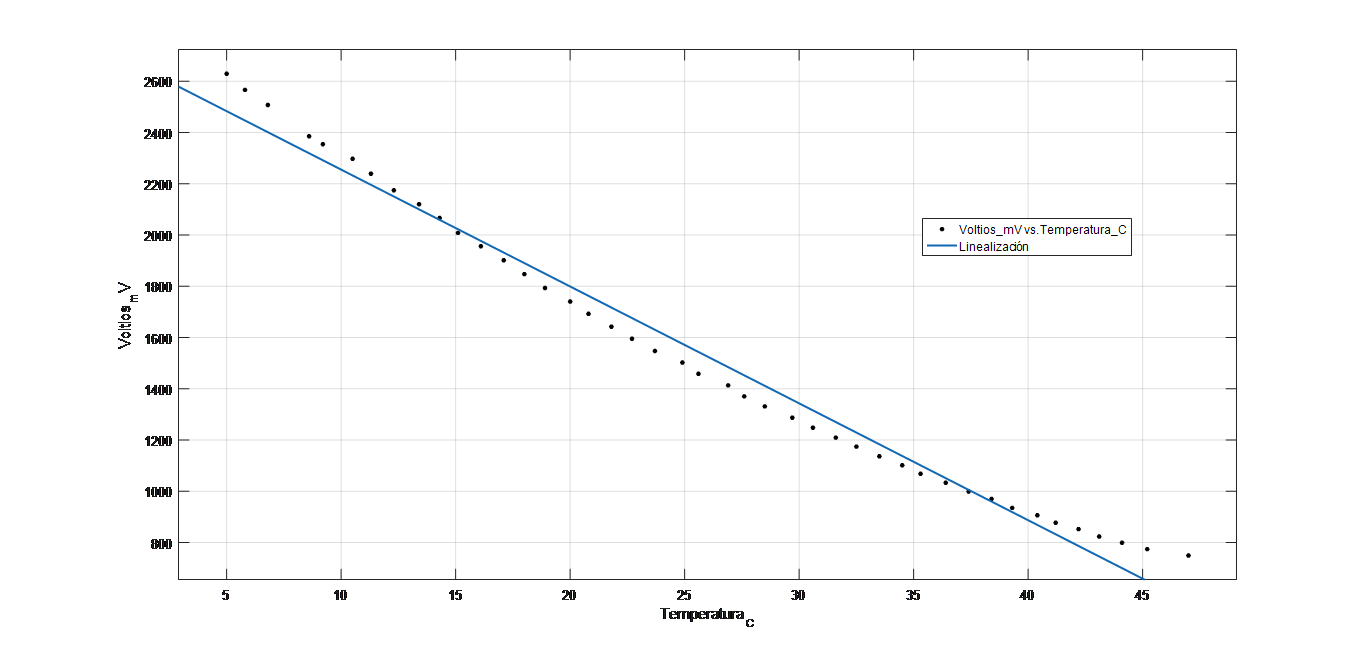
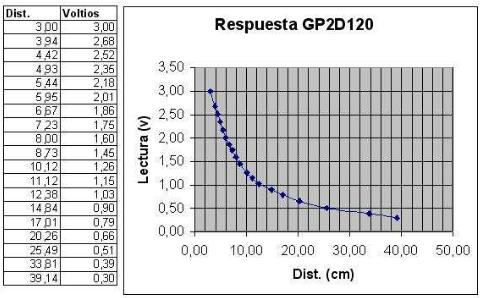
Para ello, se tomarán 4 grupos de datos, de la siguiente forma:
Primera línea recta:
Como el primer grupo tiene 5 datos, entonces N = 5.
Di |
Vi |
\( {Di}^\mathbf{2} \) |
Di * Vi |
3 |
3 |
9 |
9 |
3,94 |
2,68 |
15,5236 |
10,5592 |
4,42 |
2,52 |
19,5364 |
11,1384 |
4,93 |
2,35 |
24,3049 |
11,5855 |
5,44 |
2,18 |
29,5936 |
11,8592 |
\( \sum{D_i=}21,73 \) |
\( \sum{V_i=}12,73 \) |
\( \sum{D_i}^2=97,96 \) |
\( \sum{D_i\ast V_i}=54,14 \) |
Segunda línea recta:
Para la segunda gráfica, el grupo tiene 4 valores, entonces el valor de N = 4.
Di |
Vi |
\( {Di}^\mathbf{2} \) |
Di * Vi |
5,95 |
2,01 |
35,4025 |
11,9595 |
6,67 |
1,86 |
44,4889 |
12,4062 |
7,23 |
1,75 |
52,2729 |
12,6525 |
8 |
6 |
64 |
12,8 |
\( \sum{D_i=}27,85 \) |
\( \sum{V_i=}7,22 \) |
\( \sum{D_i}^2=196,16 \) |
\( \sum{D_i\ast V_i}=49,82 \) |
Tercera línea recta:
Para el tercer grupo de datos, el valor de N = 5.
Di |
Vi |
\( {Di}^\mathbf{2} \) |
Di * Vi |
8,73 |
1,45 |
76,2129 |
12,6585 |
10,12 |
1,26 |
102,4144 |
12,7512 |
11,12 |
1,15 |
123,6544 |
12,788 |
12,38 |
1,03 |
153,2644 |
12,7514 |
14,84 |
0,9 |
220,2256 |
13,356 |
\( \sum{D_i=}57,19 \) |
\( \sum{V_i=}5,79 \) |
\( \sum{D_i}^2=675,77 \) |
\( \sum{D_i\ast V_i}=64,31 \) |
Cuarta línea recta:
Para el cuarto grupo de datos el valor de N = 5, y sus datos quedarían así:
Di |
Vi |
\( {Di}^\mathbf{2} \) |
Di * Vi |
17,01 |
0,79 |
289,3401 |
13,4379 |
20,26 |
0,66 |
410,4676 |
13,3716 |
25,49 |
0,51 |
649,7401 |
12,9999 |
33,81 |
0,39 |
1143,1161 |
13,1859 |
39,14 |
0,3 |
1531,9396 |
11,742 |
\( \sum{D_i=}135,71 \) |
\( \sum{V_i=}2,65 \) |
\( \sum{D_i}^2=4024,60 \) |
\( \sum{D_i\ast V_i}=64,74 \) |
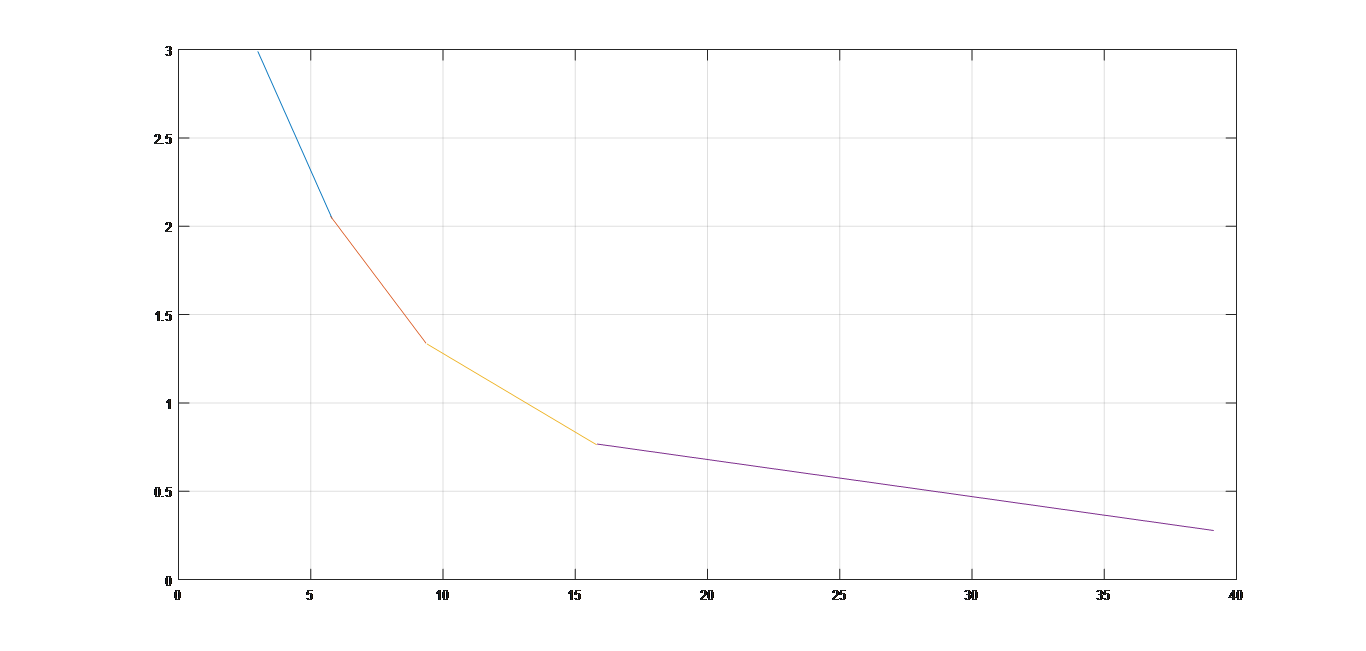
El código empleado para realizar la gráfica a trozos fue:
X1 = 3:0.1:5.8;
X2 = 5.75:0.1:9.45;
X3 = 9.4:0.1:15.85;
X4 = 15.83:0.1:39.14;
Y1 = -0.337.*X1 + 4;
Y2 = -0.199.*X2 + 3.2;
Y3 = -0.089.*X3 + 2.17;
Y4 = -0.021.*X4 + 1.1;
figure
plot(X1, Y1, X2, Y2, X3, Y3, X4, Y4);
grid on
El tutorial paso a paso puede encontrarse en la primera pestaña de este sitio web.

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional